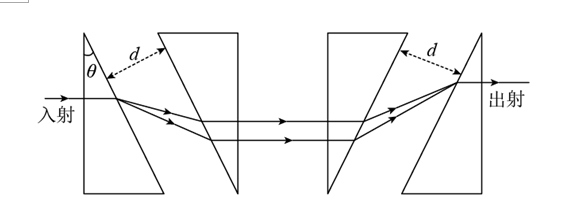
超强超短光脉冲产生方法曾获诺贝尔物理学奖，其中用到的一种脉冲激光展宽器截面如图所示。在空气中对称放置四个相同的直角三棱镜，顶角为$\theta$ 。一细束脉冲激光垂直第一个棱镜左侧面入射，经过前两个棱镜后分为平行的光束，再经过后两个棱镜重新合成为一束，此时不同频率的光前后分开，完成脉冲展宽。已知相邻两棱镜斜面间的距离 $d=100mm$，脉冲激光中包含两种频率的光，它们在棱镜中的折射率分别为 $n_1=\sqrt{2}$ 和 $n_2=\frac{\sqrt{31}}{4}$ 。取 $\sin 37^{\circ}=\frac{3}{5}, \cos 37^{\circ}=\frac{4}{5}, \frac{5}{\sqrt{7}}=1.890$ 。
(1)为使两种频率的光都能从左侧第一个棱镜斜面射出, 求 $\theta$ 的取值范围;
(2)若 $\theta=37^{\circ}$, 求两种频率的光通过整个展宽器的过程中, 在空气中的路程差 $\Delta L$ (保留 3 位有效数字)。