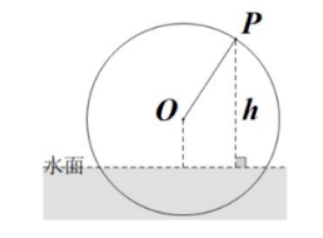
如图, 一个直径为 $5 \mathrm{~m}$ 的水车按逆时针方向每分钟转 1.8 圈, 水车的中心 $O$ 距离水面的高度 为 $1.25 \mathrm{~m}$, 水车上的盛水筒 $P$ 到水面的距离为 $h$ (单位: $m$ )(在水面下则 $h$ 为负数), 若以盛水筒 $P$ 刚浮出水面时开始计时, 则 $h$ 与时间 $t$ (单位: $s$ )
之间的关系为 $h=A \sin (\omega t+\varphi)+b\left(A>0, \omega>0,|\varphi| < \frac{\pi}{2}\right)$
(1)求 $h$ 与 $t$ 的函数解析式;
(2)求在一个旋转周期内, 盛水筒 $P$ 在水面以上的时长.