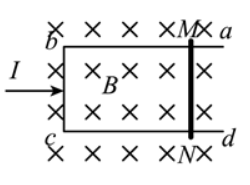
光滑绝缘平台处于竖直向下的匀强磁场中, 磁感应强度大小为 $B$ 。质量为 $m$ 的矩 形金属框 $a b c d$ 右端开口, 放在平台上。其 $b c$ 边长为 $l$, 只有 $b c$ 边有电阻且为 $R, a b 、 d c$ 足够长。质量也 为 $m$ 的薄金属片 $M N$ 置于金属框上, 与金属框间的动摩擦因数为 $\mu$, 接入金属框间的电阻也为 $R$ 。现锁 定 $M N$ ( 不能左、右运动), 用小锤给金属框一瞬时水平向右的冲量 $I$, 发现金属框能平移的距离为 $x$ 。则在这一过程中
$\text{A.}$ $M N$ 中的感应电流方向由 $N$ 到 $M$
$\text{B.}$ 通过 $M N$ 的电荷量为 $\frac{B l x}{2 R}$
$\text{C.}$ $M N$ 中产生的焦耳热为 $\frac{I^2}{4 m}-\mu m g x$
$\text{D.}$ 金属框运动的时间为 $\frac{I}{\mu m g}-\frac{B^2 l^2 x}{2 \mu m g R}$