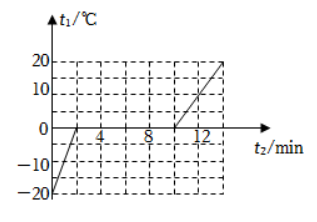
实验测得 $1 \mathrm{~kg}$ 某物质熔化时温度随时间变化的图像如图所示。已知该 物质在液态下的比热容 $c=4200 \mathrm{~J} /\left(\mathrm{kg} \cdot{ }^{\circ} \mathrm{C}\right)$, 设物质从热源吸热的功率恒定不变。在第 $10 \sim 1$ $4 \mathrm{~min}$ 内, 物质温度升高了 $20^{\circ} \mathrm{C}$, 则吸收的热量为________, 吸热功率 ________, 该物质 在固态下的比热容为 ________。