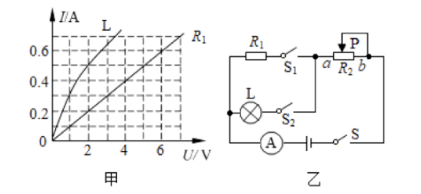
如图甲是定值电阻 $R_1$ 和标有 “ $8 \mathrm{~V} 8 \mathrm{~W}$ ” 灯泡 $\mathrm{L}$ 的 $\mathrm{I}-\mathrm{U}$ 关系图像。如图乙所示, 电源电压恒 定不变, 滑动变阻器的最大阻值为 $12 \Omega$; 当开关 $\mathrm{S} 、 \mathrm{~S}_2$ 闭合, 开关 $\mathrm{S}_1$ 断开, 将滑动变阻器 $\mathrm{R}_2$ 的滑片 $\mathrm{P}$ 滑到 $\mathrm{b}$ 端时, 灯泡 $\mathrm{L}$ 的实际功率为 $1 \mathrm{~W}$ 。求:

(1) 灯泡正常发光 10s, 电流通过灯泡产生的热量:
(2) 电源电压;
(3) 当开关 $S 、 S_1 、 S_2$ 同时闭合。调节滑片 $P$, 求电路消耗的最大功率。