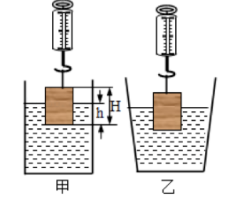
在探究影响浮力大小因素的实验中, 雷老师设计了以下实验。用测力计悬挂高 $\mathrm{H}=10 \mathrm{~cm}$ 的均匀实心铁圆柱体, 读出测力计的示数为 $\mathrm{G}$, 然后将圆柱体放入装有适量水的足够高的柱形容器中, 如图 甲所示, 稳定后读出此时测力计的示数为 $\mathrm{F}$, 计算出圆柱体所受浮力为 $\mathrm{F}$ 湾；逐步改变圆柱体下表面浸 入液体的深度 $\mathrm{h}$, 并用刻度尺测出圆柱体每次实验浸入水中前、后的液面深度, 计算出水对容器底部的 压强增加量为 $\Delta \mathrm{p}$, 并将测量结果填入表格中, 在实验的过程中, 圆柱体始终保持坚直:


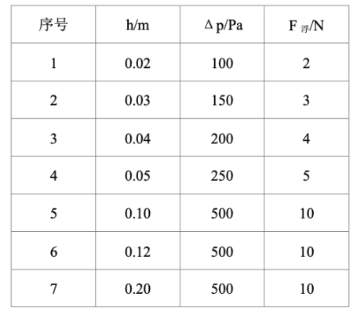
（1）实验过程中, 圆柱体所受浮力的计算式: $F_{\text {浮 }}=$ ________(用题中的字母表示)；
（2）小欣对表中实验 1 至 5 , 五组数据分析得出: 浸在液体中的物体受到的浮力与物体________ 有关;
（3）小欣将柱形容器中的水换成酒精, 重复以上实验。在 1 至 5 次实验时, 发现圆柱体下表面浸入水 中和酒精中的深度 $\mathrm{h}$ 相同时, 测力计的示数均变大了, 由此说明: 浸在液体中的物体受到的浮力还与 有关。
（4） 在圆柱形容器中加入某种液体且铁圆柱体浸入液体中体积为 $6 \times 10^{-4} \mathrm{~m}^3$ 时, 铁圆柱体受到的浮力 为 $7.8 \mathrm{~N}$, 则液体的密度为________ $\mathrm{kg} / \mathrm{m}^3$ 。
（5）请你预测当柱形容器中水的深度 $\mathrm{h}=0.06 \mathrm{~m}$ 时, 水对容器底部的压强增加量 $\Delta \mathrm{p}=$ ________ $\mathrm{Pa}$, 圆柱 体受到的浮力为 $\mathrm{F}_{\text {阊 }}=$ $\mathrm{N}$; 将盛水的柱形容器换成与柱形容器底面积相同的足喚高的梯形容器, 如图乙所示, 再将圆柱体按上述操作重复进行实验, 则水对容器底部的压强增加量 $\Delta \mathrm{p}$ ________ $300 \mathrm{~Pa}$ （选填 “大于”、“小于” 或 “等于”）。