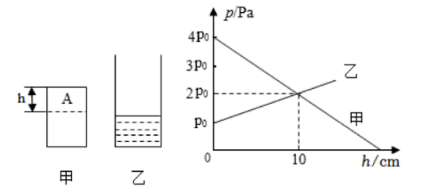
如图所示, 圆柱体甲和装有适量某液体的圆柱形容器乙的底面积之比为 $3: 4$, 把它们平放在 同一水平桌面上。在甲物体上, 沿水平方向截取一段长为 $\mathrm{h}$ 的物体 $\mathrm{A}$, 并平稳放入容器乙中, 物体 $\mathrm{A}$ 浸没于液体中（液体无溢出）。截取后, 甲、乙对桌面的压强随截取长度 $\mathrm{h}$ 的变化关系如图所示, 则当 截取 $\mathrm{h}=$________$ $ $\mathrm{cm}$ 时, 截取后的甲和乙对桌面的压强刚好相等。已知甲的密度为 $0.6 \times 10^3 \mathrm{~kg} / \mathrm{m}^3$, 容器 乙的壁厚和质量均忽略不计, 则圆柱体甲截取前对桌面的压强为________ $\mathrm{Pa}$, 乙液体的密度为 ________ $\mathrm{kg} / \mathrm{m}^3$