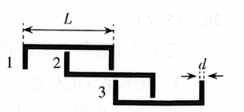
有一款推拉门, 其三扇门板俯视如图所示, 每扇门的宽度均为 $L=1.00 \mathrm{~m}$, 质量均为 $m=20 \mathrm{~kg}$, 边缘凸起部位的宽度均为 $d=0.05 \mathrm{~m}$ 。门完全关闭时, 1 号门板的左侧以及 3 号 门板的右侧分别与两侧的门框接触时, 相邻门板的凸起部位也恰好接触。测试时, 将三扇 门板均推至最左端, 然后用恒力 $F$ 水平向右推 3 号门板, 每次都经过相同的位移 $s=0.20 \mathrm{~m}$ 后撤去 $F$, 观察三扇门的运动情况。发现当恒力为 $8.5 \mathrm{~N}$ 时, 3 号门板恰好能运动到其左侧 凸起与 2 号门板右侧的凸起接触处。设每扇门与轨道间的动摩擦因数均相同, 门板凸起部位间的碰撞及门板与门框的碰撞均为完全非弹性碰撞 (不黏 连)。不考㤅空气阻力, 取 $g=10 \mathrm{~m} / \mathrm{s}^2$ 。
(1)求每扇门与轨道间的动摩擦因数。
(2)若要实现三扇门恰好完全关闭,则恒力应是多大?
(3)若想让三扇门都到达最右侧门框处, 则恒力至少是多大?