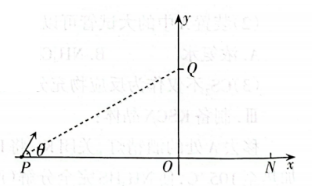
现代科技中常用电磁场分离和控制带电粒子的运动。如图所示, 在 $x O y$ 平面内,第一 象限内存在着沿 $y$ 轴负方向的匀强电场; 第二象限内, 在 $P O Q$ 三角形区域之外存在垂直于 纸面向外的匀强磁场。位于 $P(-\sqrt{3} L, 0)$ 点的粒子源, 能以不同速率、沿与 $x$ 轴夹角 $\theta=60^{\circ}$ 的同一方向发射质量均为 $m$ 、电荷量均为 $+q(q>0)$ 的 粒子, 其中速率为 $v_0$ 的粒子恰好从 $y$ 轴上的 $Q(0, L)$ 点 离开磁场, 且通过电场后到达 $x$ 轴上的 $N(L, 0)$ 点。不 考虑粒子的重力和粒子间的相互作用,求:
（1）磁感应强度的大小和电场强度的大小;
（2)速率为 $\frac{1}{2} v_0$ 的粒子到达 $x$ 轴上时的位置。