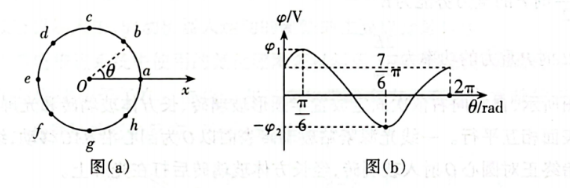
纸面内存在沿某方向的匀强电场。在电场中取 $O$ 点为坐标原点建立 $x$ 轴, 以 $O$ 为圆心、 $R$ 为半径, 从 $x$ 轴上的 $a$ 点开始沿逆时针方向作圆, $a \sim h$ 是圆周上的 8 个等分点, 如图 (a) 所示; 测量圆上各点的电势 $\varphi$ 与半径同 $x$ 轴正方向的夹角 $\theta$, 描绘的 $\varphi-\theta$ 图像如图 (b)所示,下列说法正确的是
$\text{A.}$ 电场强度的大小为 $\frac{\varphi_1+\varphi_2}{2 R}$
$\text{B.}$ $O$ 点的电势为 $\frac{\varphi_1-\varphi_2}{2}$
$\text{C.}$ $a e$ 两点的电势差为 $\frac{\sqrt{3}\left(\varphi_1+\varphi_2\right)}{2}$
$\text{D.}$ 从 $e$ 到 $f$, 电势一直降低, 从 $g$ 到 $h$, 电势一直升高