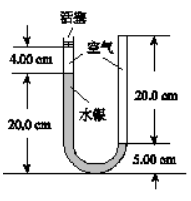
一 U形玻璃管竖直放置, 左端开口, 右端封闭, 左端上部有一光滑的轻活塞。初始时, 管内坔 柱及空气柱长度如图所示。现在左侧活塞上放置一个能产生 $69 \mathrm{cmHg}$ 压强的一个物体, 使活塞下降 $9.42 \mathrm{c}$ $m$ 。已知玻璃管的横截面积处处相同；在活塞向下移动的过程中, 没有发生气体泄漏；大气压强 $p_0=75.0 \mathrm{c}$ $m H g$. 环境温度不变。求：(结果保留3位有效数字)
(1) 右侧液柱上升的长度；
（2）右侧气体的压强；
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$