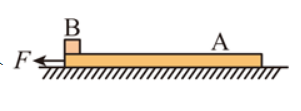
如图所示, 质量 $M=2\mathrm{kg}$ 的长木板 $A$ 静止在水平面上, 在长木板的左端放置一个可 视为质点、质量 $m=1\mathrm{kg}$ 的物体 $B$ 。开始时物体 $A、B$ 均静止, 某时刻在长木板 $A$ 的左端施加一个 水平向左的外力 $F$, 使长木板 $A$ 从静止开始做匀加速直线运动, 加速度为 $a=2\mathrm{m}/{\mathrm{s}}^2$, 当长木板 $A$的速度达到 $v=6\mathrm{m}/\mathrm{s}$ 时, 撤去外力 $F$, 最后物体 $B$ 恰好没有脱离长木板 $A$ 。已知 $A$ 和 $B$ 以及 $A$ 与地面间的动摩擦因数均为 $\mu =0.1$, 最大 静摩擦力等于滑动摩擦力, 重力加速度 $g=10\mathrm{m}/{\mathrm{s}}^2$, 试求:
(1) 长木板在加速过程中, 物体 $B$ 的加速度 $a_B$ 及水平外力 $F$ 的大小;
（2）长木板 $A$ 的长度 $L$ 。