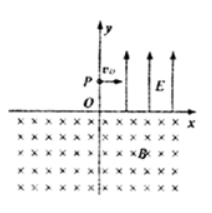
如图, 在 $x o y$ 平面内, I 象限中有匀强电场, 场强大小为 $E$, 方向沿 $y$ 轴正向, 在 $x$ 轴下方有方 向垂直于纸面向里的匀强磁场。今有一个质量为 $m$ 电量为 $e$ 的电子 (不计重力 ), 从 $y$ 轴上的 $P$ 点以初速度 $v$ 0 垂直于电场方向进入电场。经电场偏转后, 沿着与 $x$ 轴正方向成 $45^{\circ}$ 进入磁场, 并能返回到原出发点 $P$. 求:
（1）作出电子运动轨迹的示意图P点离坐标原点的距离 $h$ 。
（2）匀强磁场的磁感应强度。
（3）电子从 $P$ 点出发经多长时间第一次返回 $P$ 点?