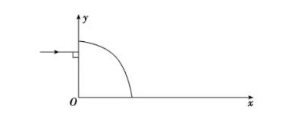
如图所示, 透明的柱形元件的横截面是半怪为 $R$ 的 $\frac{1}{4}$
圆弧, 圆心为 $O$, 以 $O$ 为原点建立直角坐标系 $x O y$.一束单色光平行于 $x$ 轴射入该元 件, 入射点的坐标为 $(0, d)$, 单色光对此元件的折射率为 $n=\frac{2 \sqrt{3}}{3}$.

(1)当d多大时, 该单色光在圆弧面上恰好发生全反射?
(2)当 $d \rightarrow 0$ 时，求该单色光照射到 $x$ 轴上的位置到圆心 $O$ 的距离. (不考虑单色 光经圆弧面反射后的情况. $\theta$ 很小时, $\sin \theta \approx \theta$ )