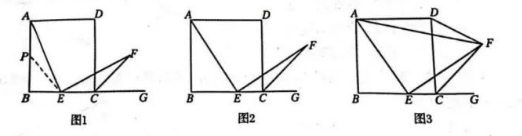
在正方形 $A B C D$ 中, $E$ 是 $B C$ 边上一点 (点 $E$ 不与点 $B, C$ 重 合), $A E \perp E F$, 垂足为点 $E, E F$ 与正方形的外角 $\angle D C G$ 的平分线交于点 $F$.
(1) 如图 1, 若点 $E$ 是 $B C$ 的中点, 猜想 $A E$ 与 $E F$ 的数量关系是 证明此猜想时, 可取 $A B$ 的中点 $P$, 连接 $E P$. 根据此图形易证 $\triangle A E P \cong \triangle E F C$. 则判断 $\triangle A E P \cong \triangle E F C$ 的依据是
(2) 点 $E$ 在 $B C$ 边上运动.
① 如图 2,(1) 中的猜想是否仍然成立? 请说明理由.
② 如图 3, 连接 $A F, D F$, 若正方形 $A B C D$ 的边长为 1 , 直接写出 $\triangle A F D$ 的 周长 $c$ 的取值范围.