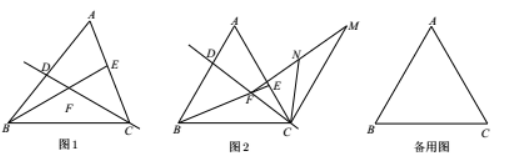
如图, 在锐角 $\triangle A B C$ 中, $\angle A=60^{\circ}$, 点 $D, E$ 分别是边 $A B, A C$ 上一动点, 连接 $B E$ 交直线 $C D$ 于点 $F$.
(1) 如图 1, 若 $A B>A C$, 且 $B D=C E, \angle B C D=\angle C B E$, 求 $\angle C F E$ 的度数;
(2) 如图 2, 若 $A B=A C$, 且 $B D=A E$, 在平面内将线段 $A C$ 绕点 $C$ 顺时针方向旋转 $60^{\circ}$ 得到线段 $C M$, 连接 $M F$, 点 $N$ 是 $M F$ 的中点, 连接 $C N$. 在点 $D, E$ 远动过程中, 猜想线段 $B F, C F, C N$ 之间存在的数量关系， 并证明你的猜想:
(3) 若 $A B=A C$, 且 $B D=A E$, 将 $\triangle A B C$ 沿直线 $A B$ 翻折至 $\triangle A B C$ 所在平面内得到 $\triangle A B P$, 点 $H$ 是 $A P$ 的中 点,点 $K$ 是线段 $P F$ 上一点, 将 $\triangle P H K$ 沿直线 $H K$ 翻折至 $\triangle P H K$ 所在平面内得到 $\triangle Q H K$, 连接 $P Q$. 在点 $D, E$ 动过程中, 当线段 $P F$ 取得最小值, 且 $Q K \perp P F$ 时, 请直接写出 $\frac{P Q}{B C}$ 的值.