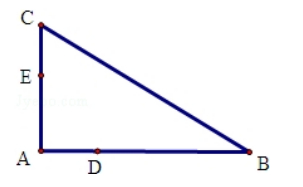
如图, $D, E$ 分别为 $\triangle A B C$ 的边 $A B, A C$ 上的点, 且不与 $\triangle A B C$ 的 顶点重合. 已知 $A E$ 的长为 $m, A C$ 的长为 $n, A D, A B$ 的长是关于 $x$ 的方程 $x^{2}-14 x+m n=0$ 的两个根.
(I) 证明：C, B, D, E四点共圆;
(II) 若 $\angle A=90^{\circ}$, 且 $m=4, n=6$, 求 $C, B, D, E$ 所在圆的半径.
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$