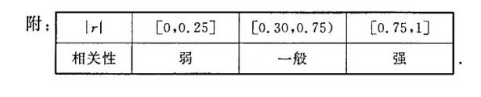
随着电池充电技术的逐渐成熟, 以锂电池为动力的新一代无绳类电动工具, 以其轻巧 便携、工作效率高、环保、可适应多种应用场景下的工作等优势, 被广泛使用. 在消费者便携无绳化需求与技术发展的双重驱动下, 锂电类无绳电动工具及配套充电器市场有望持续扩大. 某公司为适应市场并增强市场竞争力, 逐年增加研发人员, 使得整体研发 创新能力持续提升, 现对 2017 2021 年的研发人数作了相关统计, 如下图:


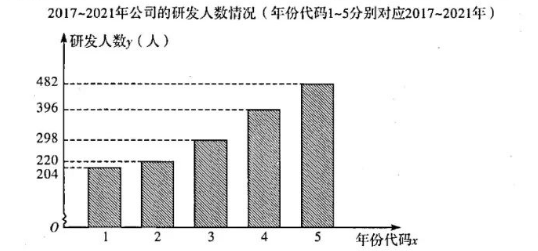
(1)根据条形统计图中数据, 计算该公司研发人数 $y$ 与年份代码 $x$ 的相关系数 $r$, 并由 此判断其相关性的强弱;
(2)试求出 $y$ 关于 $x$ 的线性回归方程,并预测 2023 年该公司的研发人数. (结果取整 娄)
参考数据 : $\sum_{i=1}^5\left(y_i-\bar{y}\right)^2=55960, \sqrt{1399} \approx 37.4$.
参考公式: 相关系数 $r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \cdot \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$.
线性回归方程的斜率 $\hat{b}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}$, 截距 $\hat{a}=\bar{y}-\hat{b} \bar{x}$.