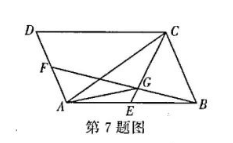
如图, 在平行四边形 $A B C D$ 中, $\overrightarrow{A B}=2 \overrightarrow{A E}, \overrightarrow{A F}=\overrightarrow{F D}$, 点 $G$ 为 $C E$ 与 $B F$ 的交点, 则 $\overrightarrow{A G}=$
A
$\frac{2}{5} \overrightarrow{A B}+\frac{1}{5} \overrightarrow{A C}$
B
$\frac{1}{5} \overrightarrow{A B}+\frac{2}{5} \overrightarrow{A C}$
C
$\frac{1}{5} \overrightarrow{A B}+\frac{4}{15} \overrightarrow{A C}$
D
$\frac{3}{10} \overrightarrow{A B}+\frac{2}{5} \overrightarrow{A C}$
E
F