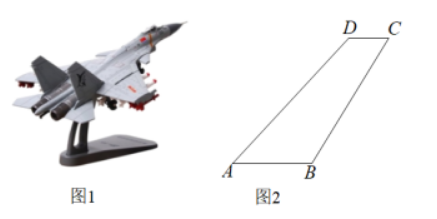
随着我国科学技术的不断发展，科学幻想变为现实.如图1是我国自主研发的某型号隐形战斗机模型，全动型后掠翼垂尾是这款战斗机亮点之 一. 图2是垂尾模型的轴切面，并通过垂尾模型的外围测得如下数据， $B C=8 ， C D=2 ， \angle D=135^{\circ} ， \angle C=60^{\circ}$ ，且 $A B \| C D$ ，求出垂尾模型 $\mathrm{ABCD}$ 的面积. (结果保留整数，参考数据: $\sqrt{2} \approx 1.414 ， \sqrt{3} \approx 1.732$ )