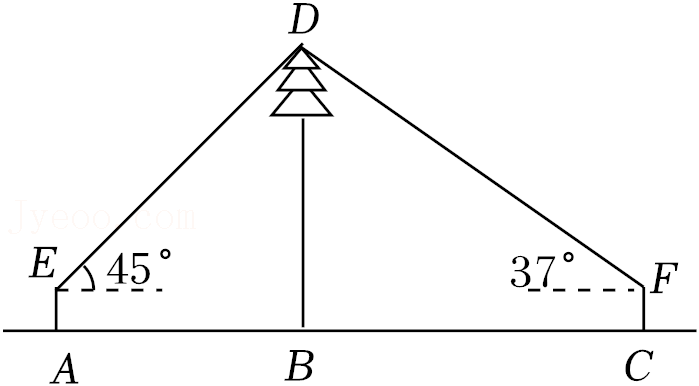
某班同学在一次综合实践课上, 测量校园内一棵树的高 度. 如图, 测量仪在 $\mathrm{A}$ 处测得树顶 $\mathrm{D}$ 的仰角为 $45^{\circ}, \mathrm{C}$ 处测得树 顶 $\mathrm{D}$ 的仰角为 $37^{\circ}$ (点 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ 在一条水平直线上), 已知测量 仪高度 $\mathrm{AE}=\mathrm{CF}=1.6$ 米, $\mathrm{AC}=28$ 米, 求树 $\mathrm{BD}$ 的高度 (结果保留 小数点后一位. 参考数据: $\sin 37^{\circ} \approx 0.60, \cos 37^{\circ} \approx 0.80, \tan 37^{\circ} \approx 0.75$