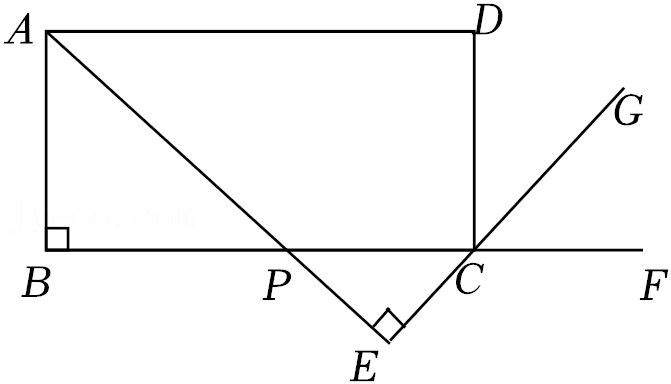
如图, 在矩形 $\mathrm{ABCD}$ 中, $\mathrm{AB}=\frac{1}{2} \mathrm{BC}$, 点 $\mathrm{F}$ 在 $\mathrm{BC}$ 边的延 长线上, 点 $\mathrm{P}$ 是线段 $\mathrm{BC}$ 上一点 (与点 $\mathrm{B}, \mathrm{C}$ 不重合), 连接 $\mathrm{AP}$ 并延长, 过点 $\mathrm{C}$ 作 $\mathrm{CG} \perp \mathrm{AP}$, 垂足为 $\mathrm{E}$.
(1) 若 $\mathrm{CG}$ 为 $\angle \mathrm{DCF}$ 的平分线. 请判断 $\mathrm{BP}$ 与 $\mathrm{CP}$ 的数量关系, 并 证明;
(2) 若 $\mathrm{AB}=3, \triangle \mathrm{ABP} \cong \triangle \mathrm{CEP}$, 求 $\mathrm{BP}$ 的长.