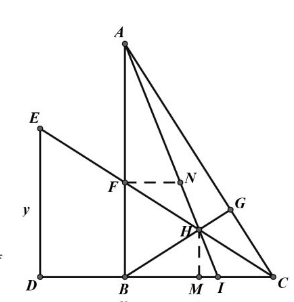
如图, $\triangle A B C \cong \triangle C D E, \angle D=\angle A B C=90^{\circ}$, 点 $B$ 在 $C D$ 上, $A B 、 C E$ 交于 $F$, 过 $B$ 作 $B G \perp A C$ 于 $G$, 交 $C E$ 于 $H$, 连接 $A H$ 并延长, 交 $C D$ 于 $I$, 设 $A B=x, B C=y$ 。 $\left(x>y\right.$ ) 求: (1) $A H$ 的长 (用 $x ， y$ 表示);（2） $\frac{B C}{I C}$ 的值。