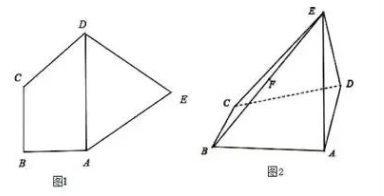
在平面五边形 $A B C D E$ 中 (如图 1), $A B C D$ 是梯形, $A D / / B C$, $A D=2 B C=2 \sqrt{2}, \quad A B=\sqrt{2}, \quad \angle A B C=90^{\circ}$,
$\triangle A D E$ 是等边三角形. 现将 $\triangle A D E$ 沿 $A D$ 折 起, 连接 $E B, E C$ 得四棱雉 $E-A B C D$ (如 图 2）, 且 $E C=2 \sqrt{2}$.
(1) 求证: 平面 $E A D \perp$ 平面 $A B C D$;
(2) 若 $F$ 是棱 $E B$ 的中点, 求 $C F$ 与平面 $A B C D$ 所成角的正切值.