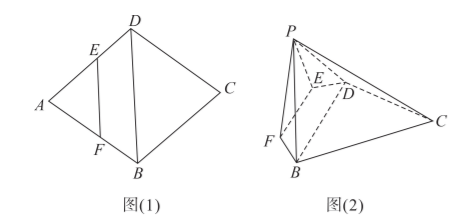
如图 (1), 菱形 $A B C D$ 中, $\angle A B C=120^{\circ}$, 动点 $E, F$ 分别在边 $A D, A B$ 上(不含端点), 且 $\overrightarrow{E F}=\lambda \overrightarrow{D B}(0 < \lambda < 1)$, 沿 $E F$ 将 $\triangle A E F$ 向上折起得到 $\triangle P E F$, 使得平面 $P E F \perp$ 平面 $B C D E F$, 如图 (2) 所示.
(1) 当 $\lambda$ 为何值时, $B F \perp P D$;
(2) 若直线 $P C$ 与平面 $B C D E F$ 所成角的正切值为 $\frac{1}{3}$, 求平面 $P E F$ 和平面 $P B D$ 夹角的 大小.