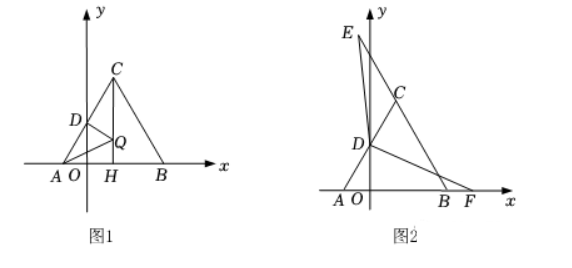
如图, 点 $\mathrm{A}(\mathrm{m}, 0), \mathrm{B}(\mathrm{n}, 0)$, 以 $\mathrm{AB}$ 为边长作等边 $\triangle \mathrm{ABC}$ 交 $y$ 轴于 $D$ 点, 且 $m, n$ 满足 $m^2+n^2+2 m-6 n+10=0$.
(1) 求 $m, n$ 的值;
(2) 如图1, 过点 $\mathrm{C}$ 作 $\mathrm{CH} \perp \mathrm{AB}$, 垂足为点 $\mathrm{H}$, 且 $\mathrm{CH}=2$, 当动点 $\mathrm{Q}$ 在线段 $\mathrm{CH}$ 上运动时, 请你求 出 $\mathrm{AQ}+\mathrm{DQ}$ 的最小值;
(3) 如图2, 点 $E$ 在线段 $B C$ 的延长线上, 点 $F$ 在线段 $A B$ 的延长线上, 当 $\angle E D F=120^{\circ}$ 时, 请问 $\mathrm{CE}-\mathrm{BF}$ 的值是否发生变化? 若改变, 请说明理由; 若不变, 请求出CE-BF的值.