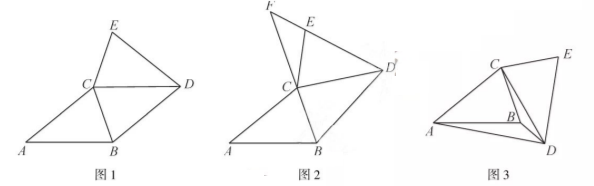
已知 $\triangle A B C \cong \triangle D E C, A B=A C, A B>B C$.
(1) 如图 1, $C B$ 平分 $\angle A C D$, 求证: 四边形 $A B D C$ 是菱形;
(2) 如图 2 , 将 (1) 中的 $\triangle C D E$ 绕点 $C$ 逆时针旋转 (旋转角小于 $\angle B A C$ ), $B C, D E$ 的延长 线相交于点 $F$, 用等式表示 $\angle A C E$ 与 $\angle E F C$ 之间的数量关系, 并证明;
(3) 如图 3, 将 (1) 中的 $\triangle C D E$ 绕点 $C$ 顺时针旋转 (旋转角小于 $\angle A B C$ ), 若 $\angle B A D=\angle B C D$, 求 $\angle A D B$ 的度数.