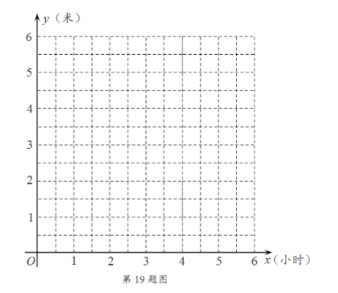
一个深为 6 米的水池积存着少量水, 现在打开水阀进水, 下表记录了 2 小时内 5 个时刻的水位高度, 其中 $x$ 表 示进水用时 (单位：小时), $y$ 表示水位高度 (单位: 米).

为了描述水池水位高度与进水用时的关系, 现有以下三种函数模型供选择: $y=k x+b(k \neq 0), y=a x^{2}+b x+c$ $(a \neq 0), \quad y=\frac{k}{x}(k \neq 0) .$
(1) 在平面直角坐标系中描出表中数据对应的点, 再选出最符合实际的函数模型, 求出相应的 函数表达式, 并画出这个函数的图象.
(2) 当水位高度达到 5 米时, 求进水用时 $x$.