如图,正方形 $\{(x, y)|| x|\leqslant 1,| y \mid \leqslant 1 \}$ 被其对角线划分为四个区域 $D_{k}(k=1,2,3,4), I_{k}=\iint_{D_{k}} y \cos x \mathrm{~d} x \mathrm{~d} y$, 则 $\max _{1 \leqslant k \leqslant 4}\left\{I_{k}\right\}=$
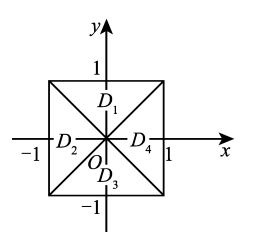
$\text{A.}$ $I_{1}$.
$\text{B.}$ $I_{2}$.
$\text{C.}$ $I_{3}$.
$\text{D.}$ $I_{4}$.