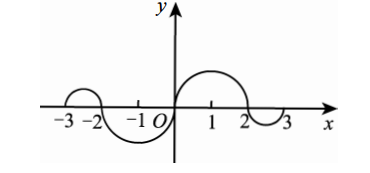
如图, 连续函数 $y=f(x)$ 在区间 $[-3,-2],[2,3]$ 上的图形分别是直径为 1 的上、下半圆周, 在 区间 $[-2,0],[0,2]$ 上的图形分别是直径为 2 的下、上半圆周. 设 $F(x)=\int_{0}^{x} f(t) \mathrm{d} t$, 则下列结 论正确的是( )
$\text{A.}$ $F(3)=-\frac{3}{4} F(-2)$.
$\text{B.}$ $F(3)=\frac{5}{4} F(2)$.
$\text{C.}$ $F(-3)=\frac{3}{4} F(2)$.
$\text{D.}$ $F(-3)=-\frac{5}{4} F(-2)$.