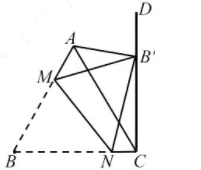
如图, 在等边 $\triangle A B C$ 中, 过点 $C$ 作射线 $C D \perp B C$, 点 $M, N$分别在边 $A B, B C$ 上, 将 $\triangle A B C$ 沿 $M N$ 折叠, 使点 $B$ 落在射线 $C D$ 上的点 $B^{\prime}$ 处, 连接 $A B^{\prime}$, 已知 $A B=2$. 给出下列四个结论: (1) $C N+N B^{\prime}$ 为定值; (2)当 $B N=2 N C$ 时, 四边形 $B M B^{\prime} N$为菱形：(3)当点 $N$ 与 $C$ 重合时, $\angle A B^{\prime} M=18^{\circ}$; (4)当 $A B^{\prime}$ 最短时, $M N=\frac{7 \sqrt{21}}{20}$. 其中正确的结论是 $\qquad$ . (填写序号)