在平面直角坐标系 $x O y$ 中, 已知点 $M(a, b), N$.
对于点 $P$ 给出如下定义: 将点 $P$ 向右 $(a \geq 0)$ 或向左 $(a < 0)$ 平移 $|a|$ 个单位长度, 再向上 $(b \geq 0)$ 或向下 $(b < 0)$ 平移 $|b|$ 个单位长度, 得到点 $P^{\prime}$, 点 $P^{\prime}$ 关于点 $N$ 的对称点为 $Q$, 称点 $Q$ 为点 $P$ 的“对应点”.
(1) 如图, 点 $M(1,1)$, 点 $N$ 在线段 $O M$ 的延长线上, 若点 $P(-2,0)$, 点 $Q$ 为点 $P$ 的“对应点”.


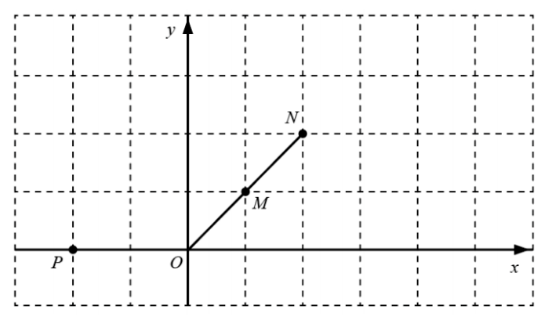
(1)在图中画出点 $Q$;
(2)连接 $P Q$, 交线段 $O N$ 于点 $T$. 求证: $N T=\frac{1}{2} O M$;

(2) $\odot O$ 的半径为 $1, M$ 是 $\odot O$ 上一点, 点 $N$ 在线段 $O M$ 上, 且 $O N=t\left(\frac{1}{2} < t < 1\right)$, 若 $P$ 为 $\odot O$ 外一点, 点 $Q$ 为点 $P$ 的“对应点”, 连接 $P Q$. 当点 $M$ 在 $\odot O$ 上运动时直接写出 $P Q$ 长的最大值与最小值的差 (用含 $t$ 的式子表 示）