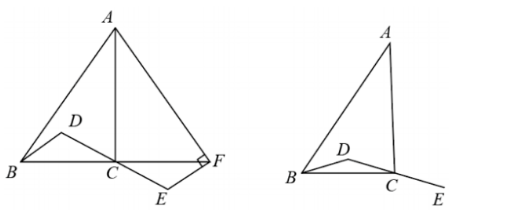
在 $\triangle A B C$ 中, $\angle A C B=90^{\circ}, D$ 为 $\triangle A B C$ 内一点, 连接 $B D, D C$, 延长 $D C$ 到点 $E$, 使得 $C E=D C$.
(1) 如图 1, 延长 $B C$ 到点 $F$, 使得 $C F=B C$, 连接 $A F, E F$. 若 $A F \perp E F$, 求证: $B D \perp A F$;
(2) 连接 $A E$, 交 $B D$ 的延长线于点 $H$, 连接 $C H$, 依题意补全图 2 . 若 $A B^{2}=A E^{2}+B D^{2}$, 用等式表示线段 $C D$ 与 $C H$ 的数量关系, 并证明.