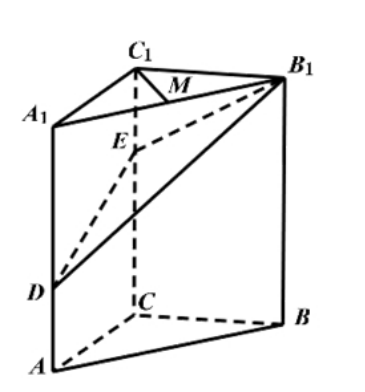
如图, 在三棱柱 $A B C-A_{1} B_{1} C_{1}$ 中, $C C_{1} \perp$ 平面 $A B C, A C \perp B C, A C=B C=2, C C_{1}=3$, 点 $D, E$ 分别在棱 $A A_{1}$ 和棱 $C C_{1}$ 上, 且 $A D=1 \quad C E=2, M$ 为棱 $A_{1} B_{1}$ 的中点.
(I) 求证: $C_{1} M \perp B_{1} D$;
( II ) 求二面角 $B-B_{1} E-D$ 的正弦值;
(III) 求直线 $A B$ 与平面 $D B_{1} E$ 所成角的正弦值.