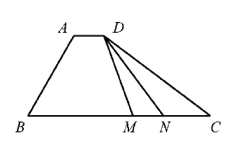
如图, 在四边形 $A B C D$ 中, $\angle B=60^{\circ}, \quad A B=3, \quad B C=6$, 且 $\overrightarrow{A D}=\lambda \overrightarrow{B C}, \overrightarrow{A D} \cdot \overrightarrow{A B}=-\frac{3}{2}$, 则实数 $\lambda$ 的值为 , 若 $M, N$ 是线段 $B C$ 上的动点, 且 $|\overrightarrow{M N}|=1$, 则 $\overrightarrow{D M} \cdot \overrightarrow{D N}$ 的最小值为