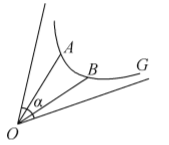
如图, 对于曲线 $G$ 所在平面内的点 $O$, 若存在以 $O$ 为顶点的角 $\alpha$, 使得对于曲线 $G$ 上的任意两个不同的点 $A, B$ 恒有 $\angle A O B \leqslant \alpha$ 成立,则称角 $\alpha$为曲线 $G$ 的相对于点 $O$ 的“界角”, 并称其中最小的“界角”为曲线 $G$ 的相对于点 $O$ 的“确界角”. 已知曲线 $C: y=\left\{\begin{array}{l}x \mathrm{e}^{x-1}+1, x>0, \\ \frac{1}{16} x^2+1, x \leqslant 0\end{array}\right.$ （其中 $\mathrm{e}$ 是自然对数的底数), 点 $O$ 为坐标原点, 曲线 $C$ 的相对于点 $O$ 的 “确界角” 为 $\beta$, 则 $\sin \beta=$