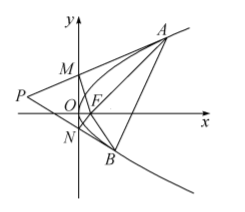
如图, $F$ 为抛物线 $C: y^2=2 p x(p>0)$ 的焦点, $O$ 为坐标原点, 过 $y$轴左侧一点 $P$ 作抛物线 $C$ 的两条切线, 切点为 $A, B, P A, P B$ 分别交 $y$ 轴于 $M, N$ 两点, 则下列结论一定正确的是
A
$\angle A P B+\angle M F N=180^{\circ}$
B
$\angle A F B+\angle A P B=180^{\circ}$
C
$\frac{|O M|}{|O N|}=\frac{|F A|}{|F B|}$
D
$\frac{|O M|}{|O N|}=\frac{|M A|}{|M P|}$
E
F