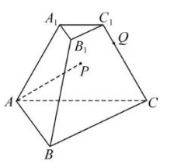
如图, 已知正三棱台 $A B C-A_1 B_1 C_1$ 的上、下底面边长分别为 2 和 6 , 侧棱长为 4 , 点 $P$ 在侧面 $B C C_1 B_1$ 内运动 (包含边界), 且 $A P$ 与平面 $B C C_1 B_1$ 所成角的正切值为 $2 \sqrt{2}$, 点 $Q$为 $C C_1$ 上一点, 且 $\overrightarrow{C Q}=3 \overrightarrow{Q C_1}$, 则下列结论中正确的有
A
正三棱台 $A B C-A_1 B_1 C_1$ 的高为 $2 \sqrt{6}$
B
点 $P$ 的轨迹长度为 $\sqrt{3} \pi$
C
高为 $\frac{4 \sqrt{6}}{3}$, 底面半径为 $\frac{\sqrt{3}}{6}$ 的圆柱可以放进棱台内
D
过点 $A, B, Q$ 的平面截该棱台内最大的球所得的截面面积为 $\frac{3}{2} \pi$
E
F