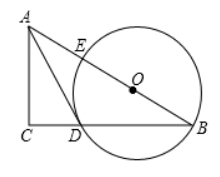
如图所示, 在 $R t \triangle A B C$ 中, 点 $O$ 在斜边 $A B$ 上, 以 $O$ 为圆心, $O B$ 为半径作圆 $O$, 分别与 $B C 、 A B$相交于点 $D 、 E$, 连接 $A D$, 已知 $\angle C A D=\angle B$;
(1) 求证: $A D$ 是 $\odot O$ 的切线;
(2) 若 $\angle B=30^{\circ}, C D=\frac{3}{2}$, 求劣弧 $B D$ 的长;
(3) 若 $A C=2, B D=3$, 求 $A E$ 的长.