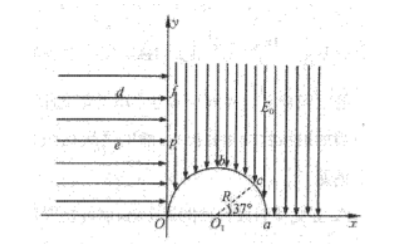
如图所示, 在平面直角坐标系 $x O y$ 的第二象限内存在沿 $x$ 轴正方向的匀强电场, 第一象限存在沿 $y$ 轴负方向, 电场强度大小为 $E_0$ 的匀强电场, $x$ 轴与半圆弧内无电场, 半圆弧的半径为 $R$, 直径 $O a$ 在 $x$ 轴上, $O_1$ 是圆心, $b$ 是半圆弧的顶点, $c$ 是半圆弧上的一点, $\angle c O_1 a=37^{\circ}$. 一质量为 $m$ 、带电量为 $q$ 的带正电粒子 (不计重力) 从第二象限的 $d$ 点[坐标为 $\left(-R, \frac{111}{50} R\right)$ ] 由静止释放, 经过 $y$ 轴上的 $f$ 点后到达半圆弧上的 $c$ 点, $\sin 53^{\circ}=0.8 、 \cos 53^{\circ}=0.6$, 求:

(1) 粒子在 $f$ 点的速度;
(2) 第二象限匀强电场的场强大小以及粒子从 $d$ 到 $c$ 电场力做的总功的平均功率;
(3) 若让该粒子从第二象限的 $e$ 点, 坐标为 $(-R, 1.5 R)$ 由静止释放, 则粒子从经过 $y$ 轴上的 $p$ 点至到达 $x$ 轴需要多少时间?