一、单选题 (共 7 题,每小题 5 分,共 50 分,每题只有一个选项正确)
设随机变量 $X, Y$ 相互独立, 且 $X \sim E(a), Y \sim E(b)(a>0, b>0, a \neq b)$, 则服从 $E(a+b)$ 的 随机变量是
$\text{A.}$ $X+Y$.
$\text{B.}$ $X Y$.
$\text{C.}$ $\max \{X, Y\}$.
$\text{D.}$ $\min \{X, Y\}$.
设 $A, B$ 是两个互不相容的事件, $P(A)>0 , P(B)>0$ ,则() 一定成立。
$\text{A.}$ $\mathrm{P}(\mathrm{A})=1-\mathrm{P}$
$\text{B.}$ $\mathrm{P}(\mathrm{A} \mid \mathrm{B})=0$
$\text{C.}$ P $(\mathrm{A} \mid \bar{B})=1$
$\text{D.}$ $\mathrm{P}(\bar{A} \bar{B})=0$
将 3 粒黄豆随机地放入 4 个杯子, 则杯子中盛黄豆最多为一粒的概率为()
$\text{A.}$ $\frac{3}{32}$
$\text{B.}$ $\frac{3}{8}$
$\text{C.}$ $\frac{1}{16}$
$\text{D.}$ $\frac{1}{8}$
设 $X$ 为一随机变量, $E(X)=1, D(X)=0.1$, 则由切比雪夫不等式一定有
$\text{A.}$ $P(|X-1| < 1) \geq 0.1$
$\text{B.}$ $P(0 < X < 2) \geq 0.9$
$\text{C.}$ $P(|X-1| \geq 1) \geq 0.9$
$\text{D.}$ $P(0 < X < 2) < 0.1$
二、填空题 (共 6 题, 每小题 5 分,共 20 分, 请把答案直接填写在答题纸上)
设 $X_1, X_2, \cdots, X_n$ 是取自总体 $X \sim N\left(\mu, \sigma^2\right)$ 的样本, 则样本均值 $\bar{X} \sim N$
设随机变量 $X$ 在区间 $[1,6]$ 上服从均匀分布,则 $P\{1 < X < 3\}=$
若离散型随机变量 $X$ 的分布律为
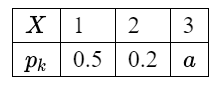
则常数 $a=$ ; 又 $Y=2 X+3$, 则 $P\{Y>5\}=$
设随机变量 $X$ 服从二项分布 $b(50,0.2)$, 则 $E(X)=$ , $D(X)=$
三、解答题 ( 共 12 题,满分 80 分,解答过程应写出必要的文字说明、证明过程或演算步骤 )
设随机变量 $X \sim N(0,1), Y=X^2+1$, 试求随机变量 $Y$ 的密度函数.
某单位有 200 台分机, 每台分机有 $5 \%$ 的时间要使用外线通话. 假定每台分机是否使用外线是相互 独立的, 试用中心极限定理估计该单位至少要装多少条外线, 才能以 $99 \%$ 以上的概率保证分机使用外线时不 等待.
(已知 $\Phi(2.33)=0.99$, 其中 $\Phi(x)$ 是标准正态分布 $N(0,1)$ 的分布函数.)
已知总体 $X$ 的分布律为
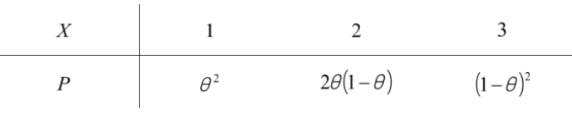
其中 $0 < \theta < 1$ 是末知参数, $\left(X_1, X_2, X_3\right)$ 是从中抽取的一个样本, 试求当样本观测值为 $\left(x_1=1, x_2=2, x_3=1\right)$ 时, 参数 $\theta$ 的最大似然估计值.
设总体 $X$ 的概率密度
$$
f(x ; \theta)= \begin{cases}1, & \theta-\frac{1}{2} \leqslant x \leqslant \theta+\frac{1}{2}, \\ 0, & \text { 其他, }\end{cases}
$$
其中 $-\infty < \theta < +\infty . X_1, X_2, \cdots, X_n$ 为取自总体 $X$ 的简单随机样本, 并记
$$
X_{(1)}=\min \left\{X_1, X_2, \cdots, X_n\right\}, X_{(n)}=\max \left\{X_1, X_2, \cdots, X_n\right\} .
$$
(1) 求参数 $\theta$ 的矩估计量 $\hat{\theta}_M$ 和最大似然估计量 $\hat{\theta}_L$;
(2) 判断 $\frac{X_{(1)}+X_{(n)}}{2}$ 是否为 $\theta$ 的无偏估计量, 并说明理由.
设 $(X, Y)$ 联合密度函数为
$$
f(x, y)=\left\{\begin{array}{cc}
6 x y^2, & 0 < y < 1, y < x < 2-y \\
0, & \text { 其他 }
\end{array}\right.
$$
试求: (I) 边缘密度函数 $f_X(x) 、 f_Y(y)$; (II) $X$ 与 $Y$ 的独立性与相关性; (III) $Z=X+Y$ 的概率密 度函数 $f_Z(z)$.
设随机变量 $X$ 在区间 $[1 , 2]$ 上服从均匀分布,
求: (1) $X$ 的分布函数 $F(x)$ :
(2) $Y=e^X$ 的概率密度 $f_Y(y)$.
设连续型随机变量 $X$ 的分布函数为
$$
F(x)=\left\{\begin{array}{cc}
A+B e^{-2 x} & x>0 \\
0 & \text { 其它 }
\end{array}\right.
$$
求 : (1) $A, B$ 的值: (2) $p(-2 < x \leq 2)$ :(3) $X$ 的概率密度函数.
一学校有 1000 名住校生,每人都以 $80 \%$ 的概率去图书馆上自习,用中心极限定理求:图书馆至少应设 置多少个座位,才能以 $99 \%$ 的概率保证去上自习的学生都有座位? $(\Phi(2.33)=0.99)$
1. 在假设检验问题中
(1)若检验结果是接受原假设, 则检验可能犯哪一类错误?
(2)若检验结甲是拒绝原假设,则检验又有可能犯哪一类错误?
2. 某厂生产的汽车电池便用寿命服从正态分布 $N\left(\mu, \sigma^2\right)$, 其说明书上写明其标准差不超过 0.9 年。现随机抽取 10 个, 得样本均值为 4 年, 样本标准差为 1.2 年。试在显著性水平 $\alpha=0.05$ 下, 检验厂方说明书上所写的标准差是否可信.
设二维随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)=\left\{\begin{array}{cc}
(2-x) y, & 0 \leq x \leq 2,0 \leq y \leq 1 \\
0, & \text { 其他 }
\end{array}\right.
$$
求: (1) 求 $X, Y$ 的边缘概率密度 $f_X(x), f_Y(y)$, 并判断 $X$ 与 $Y$ 是否相互独立(说明原因)?
(2) 求 $P\{X+Y \leq 1\}$.
设某供电区域中共有 10000 盏电灯, 夜晩每盏灯开着的概率均为 0.7 , 假设各灯开、关时间彼此独立, 求夜晩同时开着的灯的数量在 6800 至 7200 间的概 率.(其中 $\left.\Phi\left(\frac{20}{\sqrt{21}}\right) \approx \Phi(4.36)=0.999999\right)$.
设总体$X$的概率密度为
$
f(x)=\left\{\begin{array}{cc}
(\theta+1) x^\theta, & 0 < x < 1 \\
0, & \text { 其他 }
\end{array}\right.
$
其中$\theta>-1$ 是末知参数, $X_1, X_2, \ldots, X_n$ 为来白总体的一个简单随机样本, $x_1, x_2, \ldots, x_n$ 为样本值, 求 $\theta$ 的矩 估计量和极大似然估计量.