单选题 (共 6 题 ),每题只有一个选项正确
一空心导体球壳, 其内、外半径分别为 $R_1$ 和 $R_2$, 带电荷 $q$, 如图所示, 当球壳中心处再放一电荷为 $q$ 的点电荷时, 则导 体球壳的电势 (设无穷远处为电势零点) 为
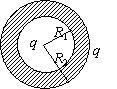
$\text{A.}$ $\frac{q}{4 \pi \varepsilon_0 R_1}$
$\text{B.}$ $\frac{q}{4 \pi \varepsilon_0 R_2}$
$\text{C.}$ $\frac{q}{2 \pi \varepsilon_0 R_1}$
$\text{D.}$ $\frac{q}{2 \pi \varepsilon_0 R_2}$
一空心导体球壳, 其内、外半径分别为 $R_1$ 和 $R_2$, 带电荷 $q$, 如图所示, 当球壳中心处再放一电荷为 $q$ 的点电荷时, 则导 体球壳的电势 (设无穷远处为电势零点) 为

$\text{A.}$ $\frac{q}{4 \pi \varepsilon_0 R_1}$
$\text{B.}$ $\frac{q}{4 \pi \varepsilon_0 R_2}$
$\text{C.}$ $\frac{q}{2 \pi \varepsilon_0 R_1}$
$\text{D.}$ $\frac{q}{2 \pi \varepsilon_0 R_2}$
有两个大小不相同的金属球,大球直径是小球的两倍,大球带电,小球不带电,两者相距很远.今用细长导线将两者相连,在忽略导线的影响下,大球与小球的带电之比为
$\text{A.}$ 2
$\text{B.}$ 1
$\text{C.}$ 1/2
$\text{D.}$ 0
如图所示,一球形导体,带有电荷q,置于一任意形状的空腔导体中.当用导线将两者连接后,则与未连接前相比系统静电场能量将
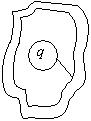
$\text{A.}$ 增大
$\text{B.}$ 减小
$\text{C.}$ 不变
$\text{D.}$ 如何变化无法确定
用力F把电容器中的电介质板拉出,在图A.和图B.的两种情况下,电容器中储存的静电能量将

$\text{A.}$ 都增加
$\text{B.}$ 都减少
$\text{C.}$ A.增加,B.减少.
$\text{D.}$ A.减少,B.增加
图示一均匀带电球体,总电荷为+Q,其外部同心地罩一内、外半径分别为r1、r2的金属球壳.设无穷远处为电势零点,则在球壳内半径为r的P点处的场强和电势为
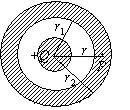
$\text{A.}$ $E=\frac{Q}{4 \pi \varepsilon_0 r^2} \quad U=\frac{Q}{4 \pi \varepsilon_0 r}$
$\text{B.}$ $E=0$,$U=\frac{Q}{4 \pi \varepsilon_0 r_1}$
$\text{C.}$ $E=0$,$U=\frac{Q}{4 \pi \varepsilon_0 r}$
$\text{D.}$ $E=0$,$U=\frac{Q}{4 \pi \varepsilon_0 r_2}$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
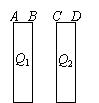
如图所示, 两块很大的导体平板平行放置, 面积都是 $S$, 有一定厚度, 带电荷分别为 $Q_1$ 和 $Q_2$. 如不计边缘效应, 则 $A$ 、 $B 、 C 、 D$ 四个表面上的电荷面密度分别为
电容为 $C_a$ 的平板电容器, 接在电路中, 如图所示. 若将相对介电常量为 $\varepsilon_r$ 的各向同性均匀电介质揷入电容器中(填满空 间), 则此时电容器的电容为原来的 ________ 偣, 电场能量是原来的 ________ 倍.
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
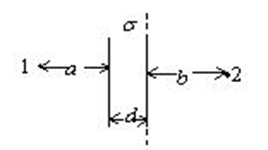
厚度为 $d$ 的“无限大”均匀带电导体板两表面单位面积上电荷之和为 $\sigma$. 试求图示离左板面距离为 $a$ 的一点与离右板面距 离为 $b$ 的一点之间的电势差.
半径分别为 $1.0 \mathrm{~cm}$ 与 $2.0 \mathrm{~cm}$ 的两个球形导体, 各带电荷 $1.0 \times 10 \mathrm{~s}$, 两球相距很远. 若用细导线将两球相连接. 求(1)每 个球所带电荷; (2)每球的电势