单选题 (共 3 题 ),每题只有一个选项正确
某车型在红绿灯停启、无保护左转、避让路口车辆、礼让行人、变道等方面都能无干预自动驾驶.某次试乘时,甲、乙两车同时并排出发,沿着同一平直路面行驶,它们的速度v随时间t变化的图像如图所示.则下列说法中正确的是
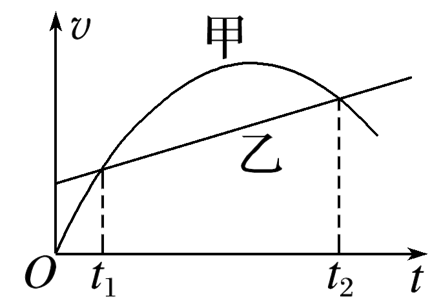
$\text{A.}$ t1~t2时间内,甲、乙两车的加速度不可能相同
$\text{B.}$ t1~t2时间内,甲、乙两车间的距离始终增大
$\text{C.}$ t1~t2时间内,甲、乙两车相遇两次
$\text{D.}$ t1~t2时间内,甲车的平均速度大于乙车的平均速度
甲、乙两辆汽车同时同地出发,沿同方向做直线运动,两车速度的平方v2随位移x的变化关系图像如图所示,下列说法正确的是
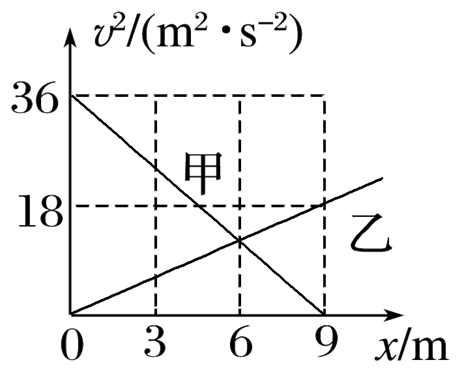
$\text{A.}$ 汽车甲停止前,甲、乙两车相距最远时,甲车的位移为8 m
$\text{B.}$ 汽车甲的加速度大小为4 m/s2
$\text{C.}$ 汽车甲、乙在t=4 s时相遇
$\text{D.}$ 汽车甲、乙在x=6 m处的速度大小为3 m/s
甲、乙两名运动员在泳池里训练,t=0时刻从泳池的两端出发,甲、乙的速度-时间图像分别如图甲、乙所示,若不计转向的时间且持续运动,两运动员均可视为质点,下列说法正确的是
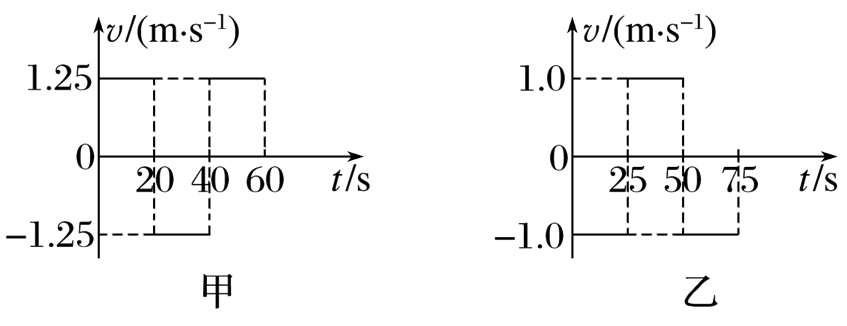
$\text{A.}$ 泳池长50 m
$\text{B.}$ 两运动员一定不会在泳池的两端相遇
$\text{C.}$ 从t=0时刻起经过1 min,两运动员共相遇了3次
$\text{D.}$ 在0~30 s内,甲、乙运动员的平均速度大小之比为8∶5
多选题 (共 4 题 ),每题有多个选项正确
如图,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位移-时间(x-t)图线,由图可知
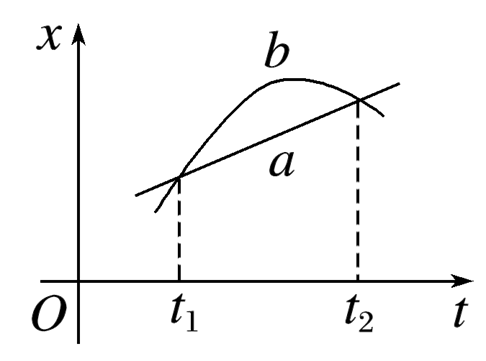
$\text{A.}$ 在t1时刻,a车追上b车
$\text{B.}$ 在t2时刻,a、b两车运动方向相反
$\text{C.}$ 在t1到t2这段时间内,b车的速率先减小后增大
$\text{D.}$ 在t1到t2这段时间内,b车的速率一直比a车大
在2017年匈牙利航海模型帆船项目世界锦标赛上,中国选手获得遥控帆船(F5-10)冠军.若a、b两个遥控帆船从同一位置向同一方向做直线运动,它们的v-t图像如图所示,则下列说法正确的是

$\text{A.}$ b船启动时,a船在其前方2 m处
$\text{B.}$ 运动过程中,b船落后a船的最大距离为1.5 m
$\text{C.}$ b船启动3 s后正好追上a船
$\text{D.}$ b船超过a船后,两船不会再相遇
近期,一段特殊的“飙车”视频红遍网络,视频中,一辆和谐号动车正和一辆复兴号动车互相追赶(如图甲).两车并排做直线运动,其v-t图像如图乙所示,t=0时,两车车头刚好并排,则
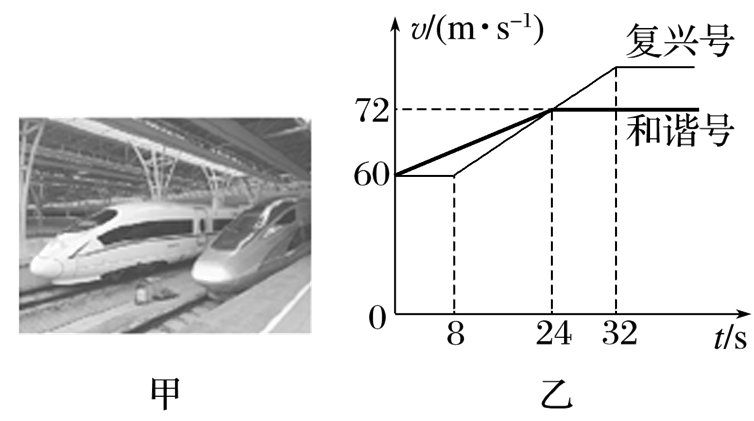
$\text{A.}$ 10 s末和谐号的加速度比复兴号的大
$\text{B.}$ 图乙中复兴号的最大速度为78 m/s
$\text{C.}$ 0到32 s内,在24 s末两车车头相距最远
$\text{D.}$ 两车头在32 s末再次并排
甲、乙两车在平直的公路上同时从同一地点同向行驶,两车的速度v随时间t的变化关系如图所示,其中两阴影部分的面积相等(S1=S2),则
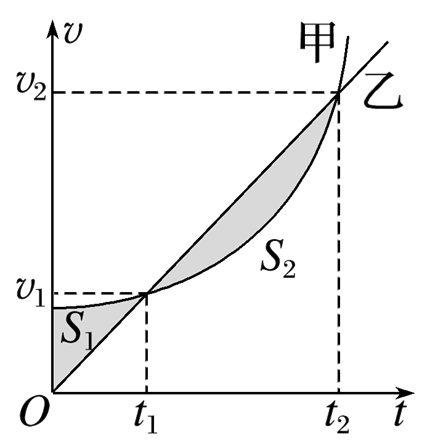
$\text{A.}$ 甲、乙两车均做直线运动
$\text{B.}$ 在0~t2时间内,甲、乙两车相遇两次
$\text{C.}$ 在0~t2时间内,甲的加速度先减小后增大
$\text{D.}$ 在0~t2时间内(不包括t2时刻),甲车一直在乙车前面
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中,某标准足球场长105 m,宽68 m.攻方前锋在中线处将足球沿边线向前路踢出,足球的运动可视为在地面上做初速度为12 m/s的匀减速直线运动,加速度大小为2 m/s2,试求:
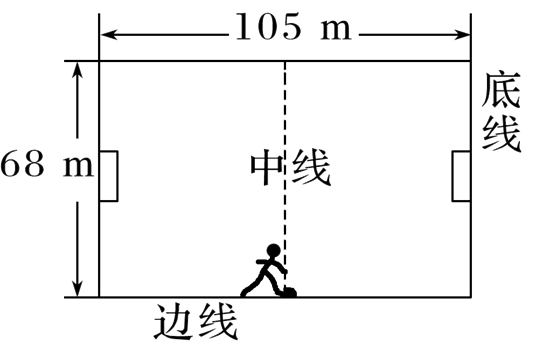
(1)足球从开始做匀减速运动到停下来的位移为多大;
(2)足球开始做匀减速直线运动的同时,该前锋队员沿边线向前追赶足球.他的启动过程可以视为初速度为零、加速度为2 m/s2的匀加速直线运动,他能达到的最大速度为8 m/s,该前锋队员至少经过多长时间能追上足球.
货车A正在该公路上以20 m/s的速度匀速行驶,因疲劳驾驶司机注意力不集中,当司机发现正前方有一辆静止的轿车B时,两车距离仅有64 m.
(1)若此时B车立即以2 m/s2的加速度启动,通过计算判断:如果A车司机没有刹车,是否会撞上B车;若不相撞,求两车相距最近时的距离;若相撞,求出从A车发现B车开始到撞上B车的时间;
(2)若A车司机发现B车,立即刹车(不计反应时间)做匀减速直线运动,加速度大小为2 m/s2(两车均视为质点),为避免碰撞,在A车刹车的同时,B车立即做匀加速直线运动(不计反应时间),问:B车加速度a2至少多大才能避免事故发生.(这段公路很窄,无法靠边让道)