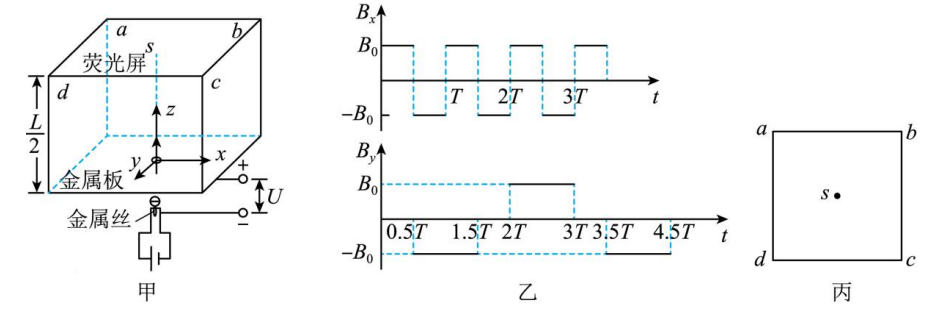
如图甲所示, 正方形荧光屏 $a b c d$ 与正方形金属板相距 $\frac{L}{2}$ 水平平行放置, 二者的边 长均为 $L_{\circ}$ 金属板的中心开有小孔,小孔正下方有一通电金属丝可持续发射热电子,金属丝 与金属板之间加有恒定电压 $U$ 。以金属板中心小为坐标原点, 沿平行于金属板两边和垂直 金属板方向建立 $x 、 y$ 和 $z$ 坐标轴, 电子从金属丝发射经小孔沿 $z$ 轴正方向射人磁场区域, 测得电子经电场加速后经过小孔时的速度大小介于 $v$ 与 $\sqrt{2} v$ 之间。 $z$ 轴与苂光屏的交点为 $s$, 金属板与苂光屏之间存在磁场 (图中未画出), 其磁感应强度沿 $z$ 轴方向的分量始终为零, 沿 $x$ 轴和 $y$ 轴方向的分量 $B_x$ 和 $B_y$ 随时间周期性变化规律如图乙所示, 图中 $B_0=\frac{2 m v}{e L}$ 。已知 电子的质量为 $m$ 、电荷量大小为 $e$, 忽略电子间的相互作用, 且电子在磁场中的运动时间远 小于磁场变化周期 $T$, 可认为电子在磁场运动过程中磁感应强度不变。求:
(1)从金属丝发射的电子的初速度大小范围;
( 2) $t=0.75 T$ 时以 $\sqrt{2} v$ 速度进人磁场的电子打在荧光屏上的位置坐标;
(3) $t=0.25 \mathrm{~T}$ 时以 $v$ 与 $\sqrt{2} v$ 速度进人磁场的两个电子打在苂光屏上时的时间差;
(4) 请在菼光屏的俯视图丙中定性画出电子在荧光屏上出现的位置。
(1)从金属丝发射的电子的初速度大小范围;
( 2) $t=0.75 T$ 时以 $\sqrt{2} v$ 速度进人磁场的电子打在荧光屏上的位置坐标;
(3) $t=0.25 \mathrm{~T}$ 时以 $v$ 与 $\sqrt{2} v$ 速度进人磁场的两个电子打在苂光屏上时的时间差;
(4) 请在菼光屏的俯视图丙中定性画出电子在荧光屏上出现的位置。
