如图所示, 电阻为 $2 R$ 、半径为 $r$ 、匝数为 $n$ 的圆形导体线圈两端与导轨 $A D 、 M N$ 相 连。与导体线圈共圆心的圆形区域内有坚直向下的磁场, 其磁感应强度随时间变化的规律如 图 2 所示, 图 2 中的 $B_0$ 和 $t_0$ 均已知。 $P T 、 D E 、 N G$ 是横截面积和材料完全相同的三根粗 细均匀的金属棒。金属棒 $P T$ 的长度为 $3 L$ 、电阻为 $3 R$ 、质量为 $m$ 。导轨 $A D$ 与 $M N$ 平行且 间距为 $L$, 导轨 $E F$ 与 $G H$ 平行且间距为 $3 L, D E$ 和 $N G$ 的长度相同且与 $A D 、 M N$ 的夹角 均为 $30^{\circ}$ 。区域 I 和区域 II 是两个相邻的、长和宽均分别相同的空间区域, 其长度均为 $d$ 。 区域 I 中存在坚直向下、磁感应强度大小为 $B_0$ 的匀强磁场。0 $2 t_0$ 时间内, 使棒 $P T$ 在区域 I 中某位置保持静止, 且其两端分别与导轨 $E F$ 与 $G H$ 对齐。除导体线圈、金属棒 $P T 、 D E$ 、 $N G$ 外, 其余导体电阻均不计, 所有导体间接触均良好且均处于同一水平面内, 不计一切摩 擦, 不考虑回路中的自感。
(1) 求在 $0 \sim 2 t_0$ 时间内, 使棒 $P T$ 保持静止的水平外力 $F$ 的大小;
(2) 在 $2 t_0$ 以后的某时刻, 若区域 I 内的磁场在外力作用下从区域 I 以 $v_0$ 的速度匀速运动到 区域 II 时, 导体棒 $P T$ 速度恰好达到 $v_0$ 且恰好进人区域 II ,该过程棒 $P T$ 产生的焦耳热 为 $Q$, 求金属棒 $P T$ 与区域 $\mathrm{I}$ 右边界的初始距离 $x_0$ 和该过程维持磁场匀速运动的外力 做的功 $W$;
(3) 若磁场运动到区域 II 时立刻停下, 求导体棒 $P T$ 运动到 $E G$ 时的速度 $v$ 。
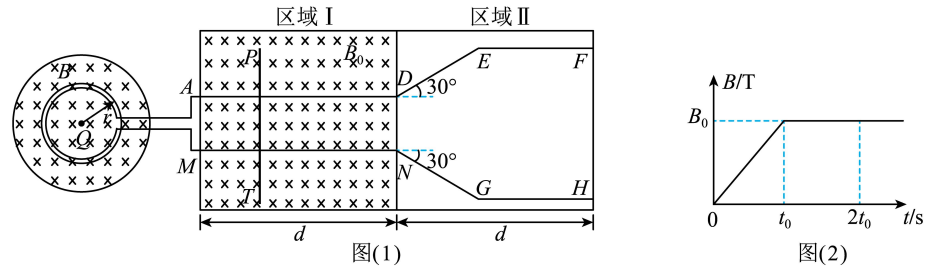
(1) 求在 $0 \sim 2 t_0$ 时间内, 使棒 $P T$ 保持静止的水平外力 $F$ 的大小;
(2) 在 $2 t_0$ 以后的某时刻, 若区域 I 内的磁场在外力作用下从区域 I 以 $v_0$ 的速度匀速运动到 区域 II 时, 导体棒 $P T$ 速度恰好达到 $v_0$ 且恰好进人区域 II ,该过程棒 $P T$ 产生的焦耳热 为 $Q$, 求金属棒 $P T$ 与区域 $\mathrm{I}$ 右边界的初始距离 $x_0$ 和该过程维持磁场匀速运动的外力 做的功 $W$;
(3) 若磁场运动到区域 II 时立刻停下, 求导体棒 $P T$ 运动到 $E G$ 时的速度 $v$ 。
