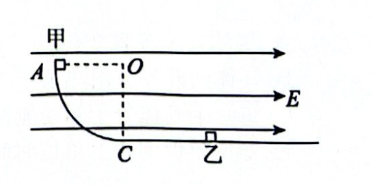
如图所示, 竖直平面内固定有圆心为 $O 、$ 半径 $R=0.12 \mathrm{~m}$ 的 $\frac{1}{4}$ 光滑圆弧轨道, 其与足够长的光滑水平面相切于最低点 $C$; 空间存在电场强度大小 $E=1 \times 10^3 \mathrm{~V} / \mathrm{m}$ 、方向水平向右的匀强电场。质量 $m_1=0.3 \mathrm{~kg}$ 、电荷量 $q=+1 \times 10^{-3} \mathrm{C}$ 的物块甲在外力作用下静止在光滑圆弧轨道的最高点 $A$, 在 $C$ 点右侧距 $C$ 点距离 $L=0.144 \mathrm{~m}$ 处放有一质量 $m_2=0.3 \mathrm{~kg}$ 、不带电的绝缘物块乙。将物块甲在 $A$ 点由静止释放, 当其落在圆弧轨道上时沿半径方向的速度减为 0 , 沿圆弧轨道切线方向的速度不变, 物块甲、乙发生碰撞为弹性碰撞。已知重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$ 。求:
(1)物块甲由 $A$ 点释放到落到圆弧轨道上经历的时间;
(2)物块甲与乙第 1 次碰撞前的速度;
(3)碰撞时间不计, 求甲、乙第 1 次碰撞后经过多长时间发生第 10 次碰撞及第 10 次碰撞后乙的速度。
(1)物块甲由 $A$ 点释放到落到圆弧轨道上经历的时间;
(2)物块甲与乙第 1 次碰撞前的速度;
(3)碰撞时间不计, 求甲、乙第 1 次碰撞后经过多长时间发生第 10 次碰撞及第 10 次碰撞后乙的速度。
