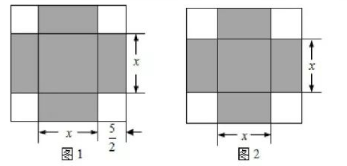
《代数学》中记载, 形如 $x^2+10 x=39$ 的方程, 求正数解的几何方法是: “如图 1 , 先构造一个面积为 $\mathrm{x}^2$ 的正方形, 再以正方形的边长为一边向外构造四个面 积为 $\frac{5}{2} \mathrm{x}$ 的矩形, 得到大正方形的面积为 $39+25=64$, 则该方程的正数解为 8 $-5=3$. ” 小聪按此方法解关于 $x$ 的方程 $x^2+6 x+m=0$ 时, 构造出如图 2 所示的 图形, 已知阴影部分的面积为 36 , 则该方程的正数解为
$\text{A.}$ $6$
$\text{B.}$ $3 \sqrt{5}-3$
$\text{C.}$ $3 \sqrt{5}-2$
$\text{D.}$ $3 \sqrt{5}-\frac{3}{2}$