科数网
题号:13586    题型:多选题    来源:河北沧州中学高三年级期中联考物理试卷
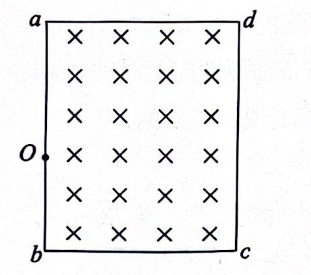
如图所示, 在矩形区域 abcd 内(包含边界)有方向垂直于纸面向里、磁感应强度大小为 B 的匀强磁场。 t=0 时刻, 位于 ab 边上 O 点的粒子源向 abcd 平面内发射出大量的同种带电粒子, 所有粒子的初速度大小相等, 方向与 Oa 边的夹角分布在 0∼180∘ 范围内且粒子均匀分布。已知 ad 边长为 L,O 点到 a、b 两点的距离分别为 115L、L2, 粒子的速率 v=qBLm, 其中 q 和 m 为粒子的电荷量和质量。沿 Ob 方向人射的粒子在 t0 时刻飞出磁场, 不计粒子重力及粒子间的相互作用力, sin⁡37∘=0.6 。下列说法正确的是
A. 粒子可能通过 c 点 B. t0=πm6qB C. 粒子在磁场中运动的最长时间为 37πm180qB D. t0 时刻, 磁场内的粒子数与发射的粒子总数之比为 1112
答案与解析：
答案仅限会员可见 微信内自动登录 或 手机登录 或 微信扫码注册登录 点击我要 开通VIP