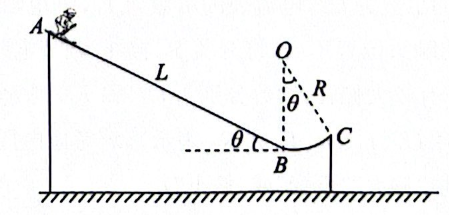
如图所示, 坚直平面内倾斜滑雪道 $A B$ 与圆弧轨道 $B C$ 在 $B$ 点平滑连接, 滑雪道倾斜轨道 $A B$长为 $L$, 倾角 $\theta=37^{\circ}, O$ 点是圆弧轨道的圆心, $O B$ 坚直, 圆弧轨道半径 $R=\frac{2}{5} L$, 圆心角也为 $\theta=37^{\circ}$ 。包含装备总质量为 $m$ 的滑雪运动员 (可视为质点) 从倾斜轨道的最高点 $A$ 由静止下滑, 最终落到水平地面上。滑雪运动员落地时速度与水平方向的夹角 $\varphi=53^{\circ}$ 。已知滑雪运动员与斜面轨道之间的动摩擦因数 $\mu=0.25$, 忽略滑雪运动员与圆弧轨道间的摩擦, 重力加速度为 $g, \sin 37^{\circ}=0.6, \cos 37^{\circ}=0.8$, 不计空气阻力, 则运动员经过圆弧轨道的 $C$ 点时对圆弧轨道的压力大小及运动员离开 $C$ 点后在空中运动的时间分别为
$\text{A.}$ $\frac{12}{5} m g \quad \frac{4}{3} \sqrt{\frac{L}{g}}$
$\text{B.}$ $\frac{12}{5} m g \quad \frac{3}{4} \sqrt{\frac{L}{g}}$
$\text{C.}$ $\frac{5}{12} m g \quad \frac{4}{3} \sqrt{\frac{L}{g}}$
$\text{D.}$ $\frac{5}{12} m g \quad \frac{3}{4} \sqrt{\frac{L}{g}}$